前不久，全球最大上市咨询公司埃森哲发布2023年技术愿景《When Atoms meet Bits》报告，并在当中深度解析到：生成式AI成为2023年四大技术发展趋势之一。 大型语言模型（Large Language Model, LLM）领域的研发和布局在国内…

10.文件与IO流 10.1 File类 文件和目录路径名的抽象表示。 文件和目录路径名的抽象表示形式。 java把电脑中的文件和文件夹（目录）封装成了一个File类，我们可以使用File类对文件和文件夹进行操作。我们可以使用File类的方法进行&#xff1…

乍看上去，马云(Jack Ma)是个有点像极客(geek)的零售商人。但在中国，这位阿里巴巴集团(Alibaba Group)49岁的创始人却有着摇滚明星一般的地位，被视为不断进取的一代人的象征。 就 像许多摇滚明星一样，马云也容易发脾气。这位前英语…

题目传送门 题目大意：10*10的地图，不过可以直接看成1*100的，从1出发，要到达100，每次走的步数用一个大小为6的骰子决定。地图上有很多个通道 A可以直接到B，不过A和B大小不确定 而且 如果99扔到100 那么只有…

2013年计算机二级、一级、三级等更多考试考前培训请进入教育联展网-中国教育培训第一门户，助您顺利通过计算机等级考试！一、选择题(每小题1分，共40分)第1题 在数据管理技术的发展过程中，经历了人工管理阶段、文件系统阶段和数据库…

这是由于工作空间损坏造成的，比如重装JDK后，或者重装Maven后这些问题。解决方法如下： 1、删除现有工作空间，重新选择一个新的。 2、重置Workspece。 3、可能是Maven版本太新导致的，与现在Eclipse不兼容，可以…

扫码查看搜索：uni-app 动态控制下拉刷新 前置条件： 开发环境：windows 开发框架：uni-app , H5，nativeJS 编辑器：HbuilderX 2.8.13 兼容版本：安卓，IOS已作测试 此代码可以直接复制到…

一、涉及内容 1.掌握SELECT语句的多表连接查询。 2.掌握SELECT语句的子查询。 二、具体操作 （一）根据Oracle数据库scott方案下的emp表和dept表，完成下列操作： 1.查询所有工种为CLERK的员工的姓名及其部门名称。 select ename,dnam…

在中国移动2020合作伙伴大会期间，中国移动研究院发布了6G系列白皮书，共三本，分别是：《2030愿景与需求白皮书（第二版）》《2030网络架构展望白皮书》《2030技术趋势白皮书》注：文末可下载6G系列白…

机房预约系统（五）教师模块1 教师登录和注销1.1 构造函数1.2 教师子菜单1.3 菜单功能实现1.4 接口对接2 查看所有预约3 审核预约教师模块 1 教师登录和注销 1.1 构造函数 在Teacher类的构造函数中，初始化教师信息，代码如下&…

文章目录功能设计：大致思路前端后端难点项目介绍需求分析主要功能选题难度和完成程度重难点分析与实现思路在 Python 中如何执行代码？如何获取运行结果的？如何获取代码异常信息？如何实现单步调试？如何可视化代码&#…

在Android中，除了从界面上启动程序之外，还可以从命令行启动程序，使用的是命令行工具am. 启动的方法为 adb shell # am start -n ｛包(package)名｝/｛包名｝.{活动(activity)名称} 第一种情…

1、编写一个函数C(n,m)求解组合数，并测试。要求用递归函数和非递归函数两种方式实现。组合数计算公式:C(n,m) C(n-1, m) C(n-1, m-1)其中：C(n,n)1 C(n,0)1import mathdef C(n,m):value math.factorial(n)/(math.factorial(m)*math.factorial(n-m))r…

作为知乎小透明一枚，今天想好好归纳写写关于国外红茶的一些事。因本人喜爱红茶，而在购买过程中经常会碰到的“应如何挑选中意的红茶”的问题，就此我想跟大家分享一下我所知道的关于国际上红茶的分级分类。众所周知，三大高香红茶里…

最好用的js前端框架、组件、文档在线预览插件

VMware以及Ubuntu的下载安装配置一、安装VMware二、开始安装Ubuntu2.1 点击创建新的虚拟机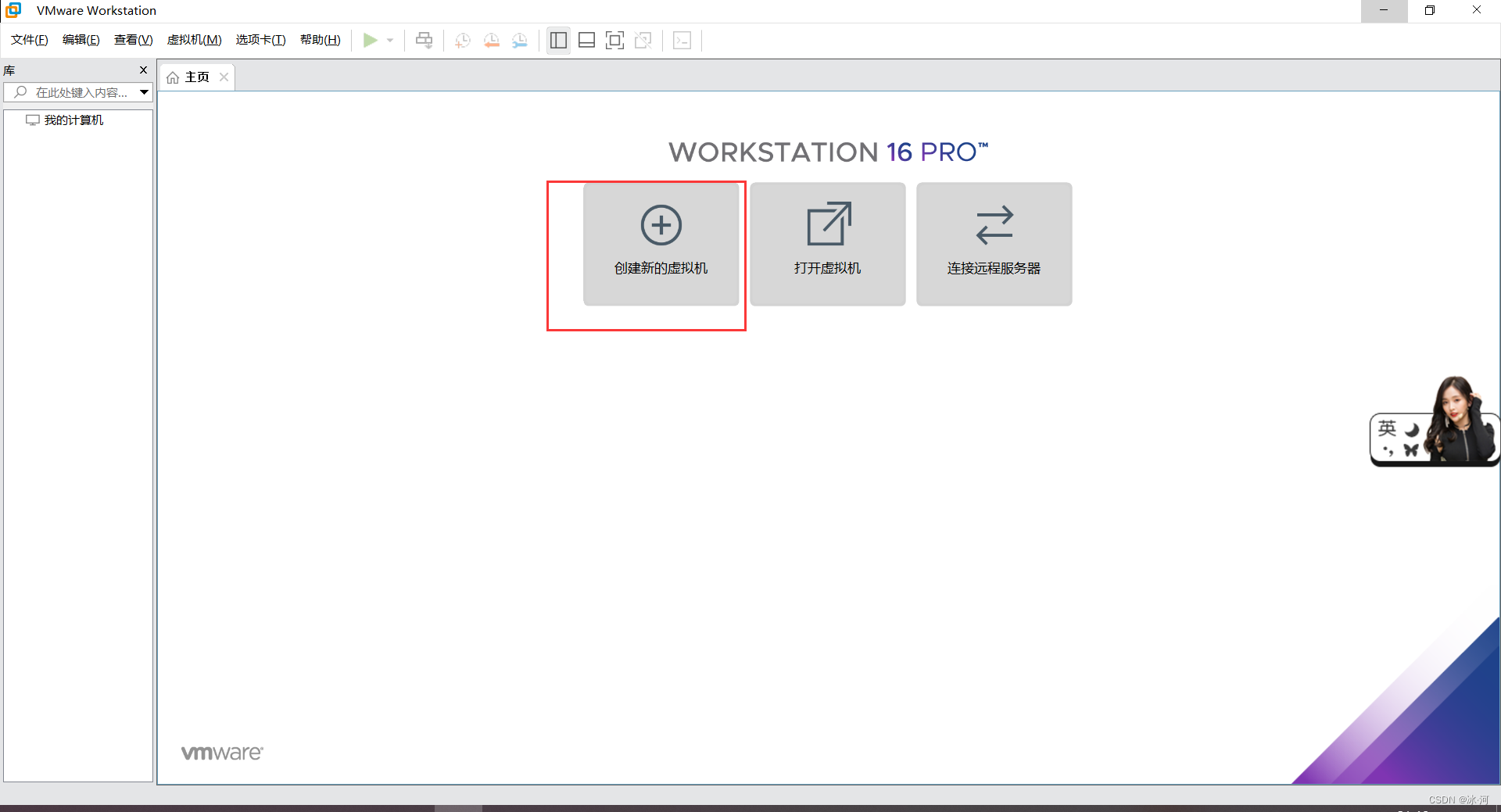2.2 选择自定义，点击下一步2.3 点击下一步2.4 选择稍后安装系统，选择…